
Stellings hus
Udadbuet eller udadhvælvet.
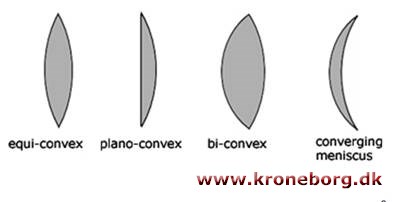
Udtrykket konveks bruges om overflader der buer udad; i
modsætning til en konkav overflade
som buer indad.
Den populære (dog ikke helt nøjagtige) definition på en
konveks funktion er en funktion som er "glad". Dette kommer
hovedsageligt fra andengradspolynomier som vender "grenene" opad (De
ligner et smil).
Både mængder og funktioner kan være konvekse, og der er
naturligvis forskel på disse definitioner. En mængde er konveks hvis uanset
hvilke to punkter vi tager i mængden og tager linjestykket mellem disse er
linjestykket fuldt indeholdt i mængden.
Mere formelt siger vi:
Lad S være en mængde i Rn S er en konveks mængde
hvis der gælder at x1, x2 ∈ S ⇒ λ x 1 + ( 1 − λ ) x 2 ∈
S , ∀
λ ∈
[ 0 , 1 ]